使える!統計講座(4)
深瀬勝範 ふかせかつのり
Fフロンティア代表取締役・社会保険労務士
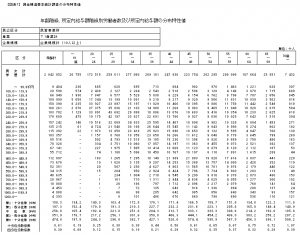
賃金構造基本統計調査には、「分布特性値」という項目があります。これを見れば、データの分布の状態や調べたいデータの全体の中での位置等が分かります。
1.分布特性値とは
賃金構造基本統計調査には、「分布特性値」という調査項目があります。分布特性値とは、データの分布の状態を数字で表したものです。これを見ると、データが固まっているのか、上下に散らばっているのかが分かります[図表7]。
クリックして拡大
分布特性値は、次の値が示されています。
(1)中位数
複数のデータを小さい順に並べたとき、すべてのデータの中間にくる値のことです。データの個数が偶数の場合は、中間にある2つの値の平均値となります。「中央値」、「メディアン」ということもあります。
(2)分位数
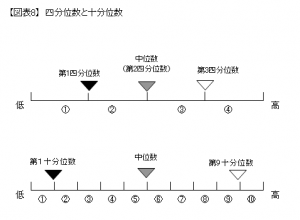
データを数値の小さい順に並べて、含まれるデータの個数が等しくなるようにいくつかの節に分けたとき、それぞれの節の境目にある数値のことをいいます。4つの節に分けるのであれば、小さいほうから順に「第1四分位数」、「第2四分位数(中位数)」、「第3四分位数」となります。賃金構造基本統計調査では、「四分位数」と「十分位数」が示されています[図表8]。
(3)分散係数
分布の広がりを示す指標で、次の算式により計算されます。
十分位分散係数=(第9十分位数―第1十分位数)/(2×中位数)
四分位分散係数=(第3四分位数―第1四分位数)/(2×中位数)
一般に、分散係数が小さいほど分布の広がりの程度が小さいことを示します。
クリックして拡大
2.分布特性値の使い方
「平均値」は、極端に高い(低い)データの影響を受けやすいという欠点があります。データの集計対象数が少なく、その中に極端に高い(低い)数字が含まれている場合等は、平均値よりも中位数のほうがデータの特徴を的確に表す数値となります。
自分の給与を分位数と比較すれば、全体のどのあたりに位置しているのかが分かります。第3四分位数を上回っているのであれば、上位25%の中にいることを意味しています。
第3四分位数と第1四分位数との間を「四分位範囲」といい、この中に全体の50%のデータが入っています。四分位分散係数は、四分位範囲の大きさ(第3四分位数-第1四分位数)を「中位数×2」で割った数値です。四分位範囲や分散係数を見れば、データの分布の状態がつかめます。
同様に、第9十分位数と第1十分位数の間には全体の80%のデータが入っていることになり、その範囲に入らないデータは相当に高い(低い)数値であることが分かります。
このように分布特性値を見れば、調べたいデータの全体の中でのおおよその位置を確認したり、データの分布の状態を数字でとらえたりできます。
3.分位数の算出の方法
自社の給与データの分位数は、Excelの関数式を使えば簡単に算出できます。第1四分位数は「=quartile(範囲,1)」で算出されます。「範囲」には集計対象となるデータが入力されている範囲を指定します。最後の「1」の代わりに「2」を入れれば中位数が、「3」を入れれば第3四分位数が算出されます。
第1十分位数は「=percentile(範囲,0.1)」で、第9十分位数は「=percentile(範囲,0.9)」で算出できます。
また、最大値は「=max(範囲)」、最小値は「=min(範囲)」で求められます。これらの関数式を使えば、自社の給与の分布状況を数字でとらえられます。
なお、賃金構造基本統計調査は、給与水準が異なる多くの会社のデータを集計したもので、四分位範囲は全労働者の給与格差を示すものです(1つの会社での給与格差のつき方を示しているわけではありません)。一般的には、1つの会社の給与格差は、全労働者のそれよりも小さくなります。自社の四分位範囲の大きさが賃金構造基本統計調査のそれよりも小さいからといって、「自社の給与格差は他社と比べて小さい」等と誤解しないようにしましょう。