使える!統計講座(9)
深瀬勝範 ふかせかつのり
Fフロンティア代表取締役・社会保険労務士
「平均」といっても、実はいくつか種類があります。代表値の中で最もよく使う平均を上手に活用することが、統計に慣れる早道です。ここでは、平均と補間について説明します。
1.相加平均と相乗平均
一般的に「平均」とは「全データの総和をデータの個数で割った値」を指します。これは、正式には「相加平均(算術平均)」といいます。
これに対して「n個のデータを掛け合わせた積のn乗根」を「相乗平均(幾何平均)」といいます。例えば、過去3年度の昇給率が「3%、5%、7%」のとき、3年間の平均昇給率は、相加平均の「5.000%(=(3%+5%+7%)÷3)」ではなく、相乗平均の「4.987%(=(3%×5%×7%)の3乗根)」となります。
「n乗根」は、エクセルでは「数値^(1/n)」と入力します(「^」はキーボードの右上のほうにあります)。上記の昇給率の場合、「=(1.03*1.05*1.07)^(1/3)」と入力します。
相乗平均は、一定期間の増加率を調べるときに使われるもので、例えば平均昇給率の計算等に使われます。
2.単純平均と加重平均
データの合計をデータ数で単純に割った平均値を「単純平均」といい、各データに重みを付けて算出した平均を「加重平均」といいます。
例えば、A社(労働者数40人)の労働者1人当たりの平均給与が30万円、B社(労働者数20人)が24万円のとき、単純平均は27万円に、加重平均では28万円になります[図表1]。つまり、単純平均は「1社当たりの平均給与」を、加重平均は「労働者1人当たりの平均給与」を表しています。

昇給や賞与(一時金)に関する統計データでは、単純平均と加重平均の両方が表示されていることがあります。各社の動向をつかみたいときには単純平均を、労働者全体の状況をつかみたいときには加重平均を見るようにします。
3.移動平均
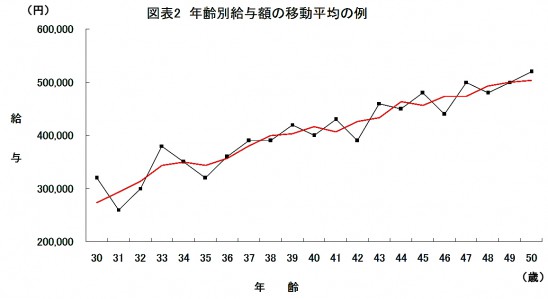
年齢ごとに平均給与を算出し折れ線グラフに表すと、ジグザグに波打った線になってしまい傾向が読み取りにくいことがあります。こういうときには、前後の年齢も含めた平均値を算出して、ジグザグをならしたグラフにすると見やすくなります。このように前後の階級も含めて平均を算出することを「移動平均法」といいます[図表2]。ある階級を中心に前後1階級のデータも含めて平均を算出することを「3項移動平均」、前後2階級も含めることを「5項移動平均」といいます。
移動平均は、上記のような場合以外にも、短期的に増減を繰り返すデータの長期的な傾向をとらえるとき等に使われます。
4.線形補間(直線補間)
38歳の給与データを知りたいときに、35歳と40歳の給与データ(それぞれ30万円、45万円とする)しか入手できなかったとします。この場合、35歳と40歳の給与データから38歳の値を算出しなければなりません。このように複数のデータが分かっているとき、それらの間にあるデータを算出することを「補間」といいます。
35歳から40歳まで一定額ずつ給与が増えていくものと仮定すると、38歳の給与は、39万円(=30万円+(45万円-30万円)×(38-35)/(40-35))となります。
厚生労働省「賃金構造基本統計調査」では、20~24歳、25~29歳・・・といった階級ごとに平均年齢と給与が示されており、「23歳」の給与データは入手できません。このようなときには、20~24歳と25~29歳の平均年齢と給与を線形補間で加工して23歳のデータを算出します。
元データの場合では分析がしにくい場合、あるいは自分がほしいデータが入手できない場合には、移動平均や線形補間等の手法を使って統計データを加工することが必要となります。これらのデータの加工は、エクセルを使えば簡単にできますので、積極的に使ってみてください。