使える!統計講座(10)
深瀬勝範 ふかせかつのり
Fフロンティア代表取締役・社会保険労務士
「年齢に応じて給与がどのように増えていくか」というように2つのデータの関係を調べるときには「回帰分析」を行います。複雑な計算を必要とする回帰分析も、パソコンを使えば簡単にできます。
1.相関とは
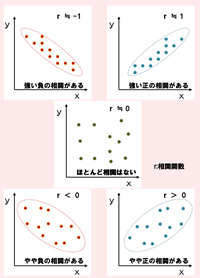
「年齢に応じて給与が増加する」というように、2つのデータの関係のことを「相関」といいます。一方のデータが増加したときに他方のデータも増加する場合を「正の相関」、逆に一方のデータが増加したときに他方のデータが減少する場合を「負の相関」といいます。
相関の強さは「相関係数」で示されます。相関係数は、-1から1までの数値をとり、「-1」に近いほど負の相関が強く、逆に「1」に近いほど正の相関が強いことを示します。また、相関係数が「0」ならば2つのデータの間には関係がないということになります。
相関が強い場合、2つのデータを関係づける要因があるものと考えることもできます。例えば、「年齢と給与との間に強い正の相関が見られる」のであれば、年齢によって給与が決まる仕組みを採用しているものと考えられます。
図表1 データの分布と相関係数(クリックして拡大)
2.相関係数の算出方法
相関係数(正式には「ピアソンの積率相関係数」といいます)はエクセルを使えば簡単に算出することができます。
分析対象となる2つのデータをワークシートに入力して、「=PEARSON(xのデータ範囲,yのデータ範囲)」という関数式を入力すれば相関係数が表示されます。
いくつ以上の相関係数を強いとするか、一概には言えませんが、一般的には、係数0.7以上(または-0.7以下)を「相関が強い」としています。年齢、勤続年数、地域の物価水準など、さまざまなデータと給与の相関係数を算出してみると、給与が何に基づいて決められているのかが分かります。
3.回帰分析とは
一方のデータと他方のデータとの関係を方程式で表す統計的手法が「回帰分析」です。回帰分析によって2つのデータの関係を方程式で示すことができれば、一方のデータが分かれば他方のデータがいくつになるか推計することができます。
例えば、多くの労働者のデータを集めて、年齢(x)と給与(y)について回帰分析を行ったところ、「y = 7000 x + 80000」という方程式が導き出されました。この場合は、20歳ならば22万円、40歳ならば36万円の給与になるものと推計できます。
回帰分析は「最小二乗法」という方法で方程式を求めます。これは、実際のデータと方程式で求めた数値との差の二乗の合計値を最小にするという考え方に基づいています。複雑な計算が必要とされる方法ですが、エクセルが回帰分析に必要な計算を自動的に行ってくれるので、だれでも簡単にできます。
4.回帰分析の進め方
エクセルで回帰分析を行う方法はいくつかありますが、ここでは散布図の作成から回帰分析を行う方法を紹介します。データは年齢と給与のデータを使います。
Excelの画面はクリックして拡大できます。
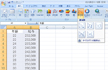
| ①年齢と給与のデータを入力して、メニューバーから「挿入」→「グラフ」→「散布図」を選択する。②表示された散布図上の任意の点をクリックする。表示されたメニューバーから、「近似曲線の追加」を選択する。
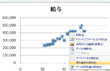
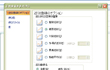
「近似曲線のオプション」では「線形近似」を選択し、「グラフに数式を表示する」と「グラフにR-2乗値を表示する」にもチェックを入れる。 ③散布図上に、年齢(X)と給与(Y)の関係を示す回帰式が表示される。 さらに、回帰式の当てはまりの良さを示す「R-2乗値(決定係数)」も表示される。 |
①エクセルに、各労働者の年齢と給与のデータを入力します。年齢と給与のデータの入力範囲を指定し、グラフ機能を使って「散布図」を作成します。
②散布図上の任意の点を右クリックして、表示された画面から「近似曲線の追加」を選択します。メニュー画面から「線形近似」を選択し、「グラフに数式を表示する」、「グラフにR-2乗値を表示する」にチェックを入れて、「閉じる」をクリックします。
③散布図上に年齢と給与との関係を示す直線(回帰直線)と方程式(回帰式)、さらにR-2乗値が表示されます。
回帰式「y = ax + b」のxに年齢を代入すれば、給与(y)を算出できます。
「R-2乗値」は、「説明係数(決定係数)」または「寄与率」といわれるものです。これは0から1までの数値をとり、1に近いほど回帰式がxとyの関係を適切に表現している(回帰式がうまく当てはまっている)ことを示します。
回帰分析は、データ分析のさまざまな場面で使えます。次回は、モデル賃金の算出を例に挙げて、回帰分析の活用方法を具体的に見ていくことにします。