使える!統計講座(11)
深瀬勝範 ふかせかつのり
Fフロンティア代表取締役・社会保険労務士
「回帰分析ができるようになったけど、どういうときに使えばよいのか分からない」という人がいるかもしれません。ここでは回帰分析を使ったモデル賃金の作成について説明しましょう。
1.モデル賃金とは
モデル賃金とは、特定の条件における標準的な給与支給額のことです。年齢別モデル賃金といえば、「20歳で18万円、30歳で32万円…」のように年齢ごとの標準的な給与を示します。
モデル賃金には「理論モデル賃金」と「実在者モデル賃金」の2種類があります。理論モデル賃金とは、特定の条件の給与支給額を規程や給与表等に基づいて算出されるものです。一方、実在者モデル賃金とは、特定の条件に該当する労働者に実際に支給している給与支給額から算出されるものです。
2.平均値を使った実在者モデル賃金の算出
実在者モデル賃金の算出方法として、年齢ごとの平均値を示すことがまず考えられます。ところが、平均値の場合、給与が極端に高い(低い)人がいると、その年齢だけモデル賃金が高く(低く)なってしまいます。また、平均値は実在するデータを集計するものですから、労働者がいない年齢についてはモデル賃金が算出できません。
そこで回帰分析を使います。回帰分析は、データの全体的な傾向からモデル賃金を算出するので極端なデータの影響を受けにくく、また、方程式が導き出せれば実際には労働者がいない年齢についてもモデル賃金を算出することができます。
3.回帰分析によるモデル賃金の算出
エクセルを使った回帰分析は、前回説明しました。ここでは、その結果を用いて実在者モデル賃金を算出します。
年齢と給与の回帰分析を行い、「y = 6619 x + 78781」という回帰式が得られました。この式でxは年齢、yは給与を示すものなので、xに年齢を入力すれば給与yが出ます。20、25、30…と年齢を入力した列の隣に「=6619*[年齢を入力したセル]+78781」という式を入れれば、年齢ごとのモデル賃金を示した一覧表ができます。
さて、ここまでは、「線形近似」という回帰分析の方法を使ってモデル賃金を算出してきました。この方法は年齢上昇に伴って直線的に給与が増えていくことを前提としています。ところが、多くの場合、給与の増え方は、若年層と高齢者は小さく、30歳から50歳くらいまでの中堅層が大きいという「S字カーブ」を描きます。したがって、線形近似を使ったモデル賃金では、若年層と高齢者の部分が実際の金額と大きくズレてしまいます。
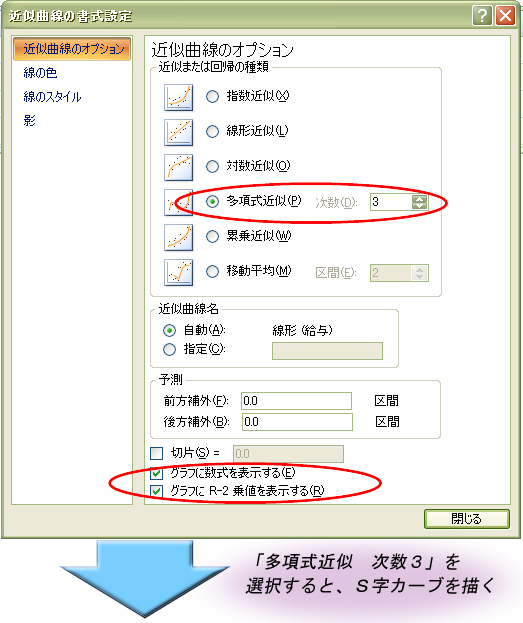
こういう場合は「線形近似」ではなく「多項式近似」を選択して、S字カーブにそった回帰式を算出します。エクセルの「近似曲線のオプション」の画面の「多項式近似」にチェックを入れ、「次数」を「3」としましょう。こうするとxとyの関係を表す方程式「y = -6.9986x3 + 809.45x2 - 22904x + 417584」が表示されました。この式のxに年齢を入れて、モデル賃金を算出します。なお、「x3」は、エクセルの式では「x^3」または「x*x*x」と入力します。
4.回帰分析の応用例
回帰分析を使ったモデル賃金は、データ全体の傾向から導き出されるものなので、ある年齢に極端に高い(低い)データがあっても、その影響をあまり受けずに滑らかな曲線が描かれます。また、従業員がいない年齢についてもモデル賃金を算出することができます。例えば、40歳以下の従業員のデータしかなくても、50歳、60歳の従業員の給与を推計できます。若い社員が多い会社が将来の人件費負担を予測するときは、こういう方法が役に立ちます。
回帰分析は、給与分析以外にも、さまざまな場面で使うことができます。例えば、売上高と従業員数との関係を回帰式で表すことができれば、今後、売上高が増加したとき、新たに採用しなければならない従業員数を算出することができます。急成長を遂げている会社は、このような分析に基づいて採用計画を策定するとよいでしょう。
回帰分析は、2つのデータ群について、一方のデータが変化したときに他方がどうなるかを推測することができます。パソコンの表計算ソフトを使えば簡単にできるので、是非、活用してみてください。